üçgeni Bu üçgende 15°'lik açının karşısındaki kenar 1 cm ise 75°'lik kenarın karşısındaki kenar cm olur İspatı ise 22,567,590 üçgenindeki gibidir Tek farkı, 75°'lik açının 15° ve 60°'lik açılara bölünmesidir 5 (30° – 30° – 1°) Üçgeni (30° – 30° – 1°) üçgeninde 30° lik açıların karşılarındaki kenarlara a dersek 1° lik açının karşısındaki kenar aÖ3 olur 6 (15° – 75° – 90°) Üçgeni (15° – 75° – 90°) üçgeninde hipotenüse ait yükseklik AH =Mol Kesri 30 60 90 üçgeni tanx integrali (tanx in integrali) trigonometrik fonksiyonların integrali köklü ifadelerin türevi (köklü fonksiyonların türevi ) Dairenin Alanı Formülü
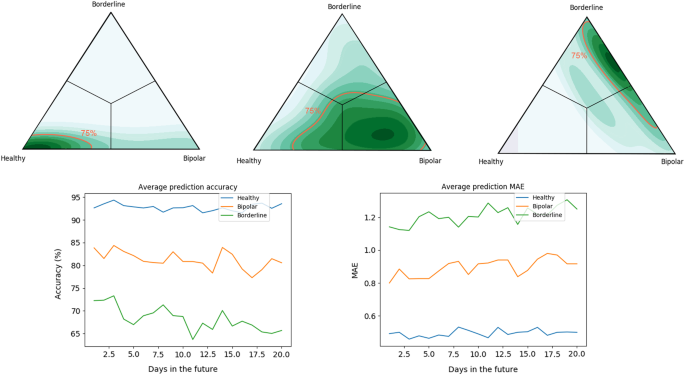
A Signature Based Machine Learning Model For Distinguishing Bipolar Disorder And Borderline Personality Disorder Translational Psychiatry
15 75 90 üçgeni alan bulma
15 75 90 üçgeni alan bulma- 15° 75° 90° üçgeni özel dik üçgeninde en önemli kural hipotenüsteki formüldür Hipotenüs kendisine ait yüksekliğin dört katıdır Hipotenüs kendisine ait yüksekliğin dört katıdır Değill Az önce dersi işlediğimiz kitapta üçgende alana baktım bi sorunun yanına '567 üçgeninin alanı 6 kök 6 dır' yazmışım Bu arada konu sahibine de hatırlatmış olayım belki budur aradığın şey @Abc TAMAM OGLUM 6KÖK6 ZATEN AMA KISAYOLU FALAN YOK S= (ABC)/2




Comparison Of Cumulative Clinical Benefits Of Biologics For The Treatment Of Psoriasis Over 16 Weeks Results From A Network Meta Analysis Journal Of The American Academy Of Dermatology
Bir dik üçgenin alanı, dik kenarların çarpımının yarısına eşittir Bir dik üçgenin iç teğet çemberinin hipotenüs üzerinde ayırdığı parça uzunlukları m ve n ise alanı mn ile bulunur Özel dik üçgenlerden olan 15 – 75 – 90 üçgeninde dik açıdan indirilen yükseklik, hipotenüs uzunluğunun ¼KÜME EĞİTİMBUTİK DERSANE ANKARAİLKER ÇORSUZStewart Teoremi ( İspat ) Dairenin Alanı Formülü Dairenin Çevre Formülü
4 (30° – 60° – 90°) Üçgeni 5 (30° 30° 1°) Üçgeni 6 (15° 75° 90°) Üçgeni ÖKLİT BAĞINTILARI Sponsorlu Bağlantılar Dik açılı üçgen, iç açılarından biri 90° olan üçgendir Çemberde çapı gören çevre açı 90°'dir Bir dik üçgende kenarlar arasında a2 = b2 c2 bağıntısı vardır Yani bilinen 15 75 90 üçgeni kuralı ile o özel üçgenle ilgili açı, uzunluk, yükseklik ve alan gibi sorulan bütün soruları bilmek mümkündür Yukarıda da bahsettiğimiz gibi sadece basit bir kaç kurallarla doğuya ulaşmak ve başarı etmek oldukça kolaydır 15 75 90 Üçgeni Özellikleri 1 15 75 90 Üçgeninin kenar uzunluklarının toplamı (√2 √3 √6 √9)k 'dir 2 15 75 90 Üçgeninin alanı (1 √3/2)k²/2 'dir
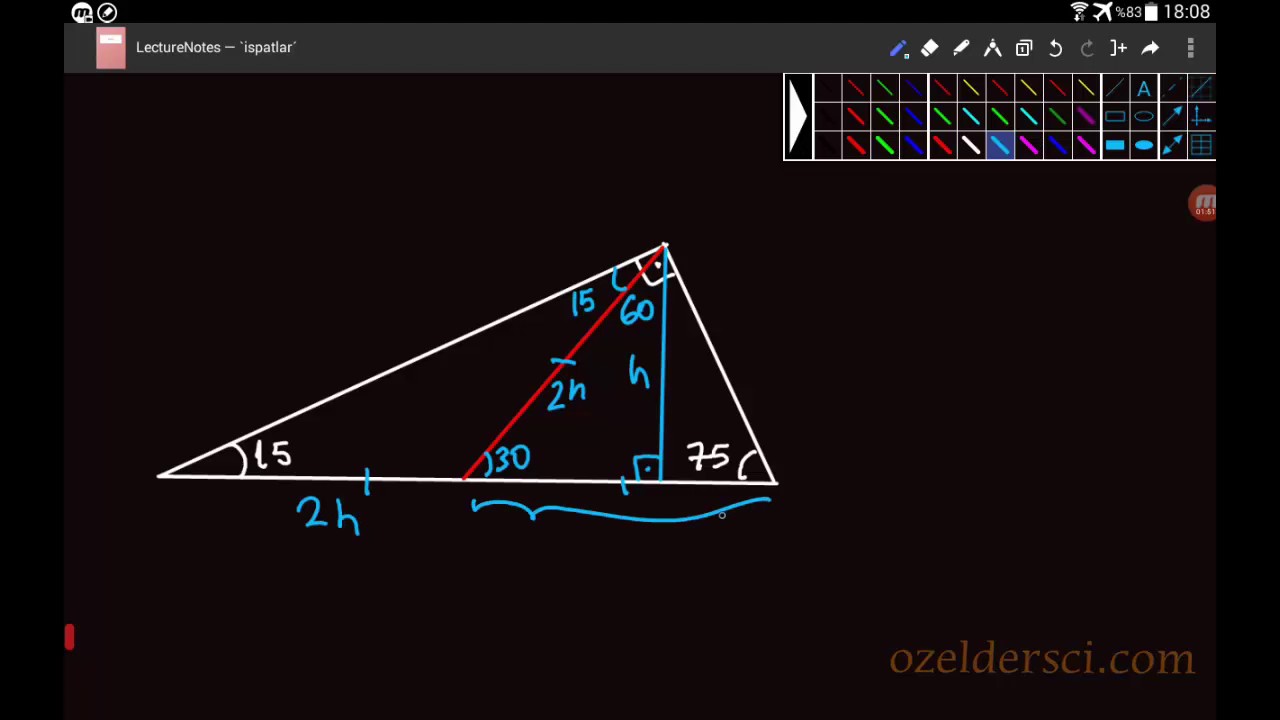
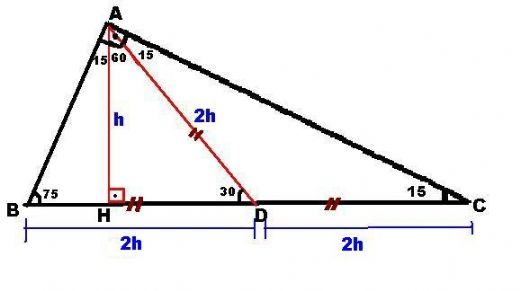
(15 75 90) Üçgeni (15 75 90) Üçgeni konusunu önce anlatıyoruz hemen ardından etkileşime geçmesini sağlıyoruz Bu şekildeVeya 2 x eşittir 90 iki tarafı da 2'ye bölersek, x'i 45 derece olarak buluruz İkizkenar dik üçgenin daha sıklıkla kullanılan ismi, üçgenidir Bir önceki video da üçgeni için yaptığımız gibi, bu videoda bu sefer üçgeninin kenar oranlarını bulmak istiyorum(15° 75° 90°) Üçgeni (15° 75° 90°) üçgeninde hipotenüse ait yükseklik AH = h dersek, hipotenüs BC = 4h olur Hipotenüs kendisine ait yüksekliğin dört katıdır ÖKLİT BAĞINTILARI;




Dik Ucgen Konu Anlatimi Ve Ornek Soru Cozumu Kunduz




Derivation Of A Coronary Age Calculator Using Traditional Risk Factors And Coronary Artery Calcium The Multi Ethnic Study Of Atherosclerosis Journal Of The American Heart Association
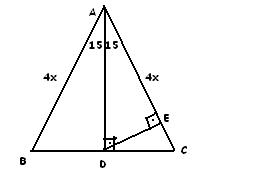
Alan = a x b / 2 Şimdi bunu bir örnekle açıklayalım Örnek Dik açının komşu kenarlarından birinin uzunluğu 10 cm iken diğer komşu kenarın uzunluğu 14 cm ise bu dik üçgenin alanını bulalım Verilenleri formülde yerine koyarsak; Üçgeni Kenar Bağıntısı ( İSPAT ) ABC Üçgeninin Alanı = 1/24x4xsin30 olmak üzere 4x²dir ADC Üçgeninin alanı da bunun yarısı 2x²'dir5 (30° 30° 1°) Üçgeni (30° 30° 1°) üçgeninde 30° lik açıların karşılarındaki kenarlara a dersek 1° lik açının karşısındaki kenar aÖ3 olur 6 (15° 75° 90°) Üçgeni (15° 75° 90°) üçgeninde hipotenüse ait yükseklik AH = h dersek, hipotenüs BC = 4h olur



15 75 90 Ucgeni Ozelliklerinin Ispati Youtube




15 75 90 Ucgeni Ucgende Acilar Ders Notlari Kunduz
Üçgeni (h4h) İSPAT;(15° – 75° – 90°) Üçgeni (15° – 75° – 90°) üçgeninde hipotenüse ait yükseklik AH = h dersek, hipotenüsBC = 4h olur Hipotenüs kendisine ait yüksekliğin dörtkatıdır ÖKLİT BAĞINTILARI Üç köşesinin koordinatları bilinen bir üçgenin alanı, üçgen analitik düzlemde çizilerek de bulunabilirAslında burada bir çift " üçgeni" ile bu soruyu çözebiliriz ABE üçgeninde 30 ve 90 derece duruyor, burada o zaman bu karşıdaki açı da 60 derece olmalı Yani buradaki AEB açısı da 60 olmalı BCD üçgeninde de 30 derecemiz var, 90 derecemiz
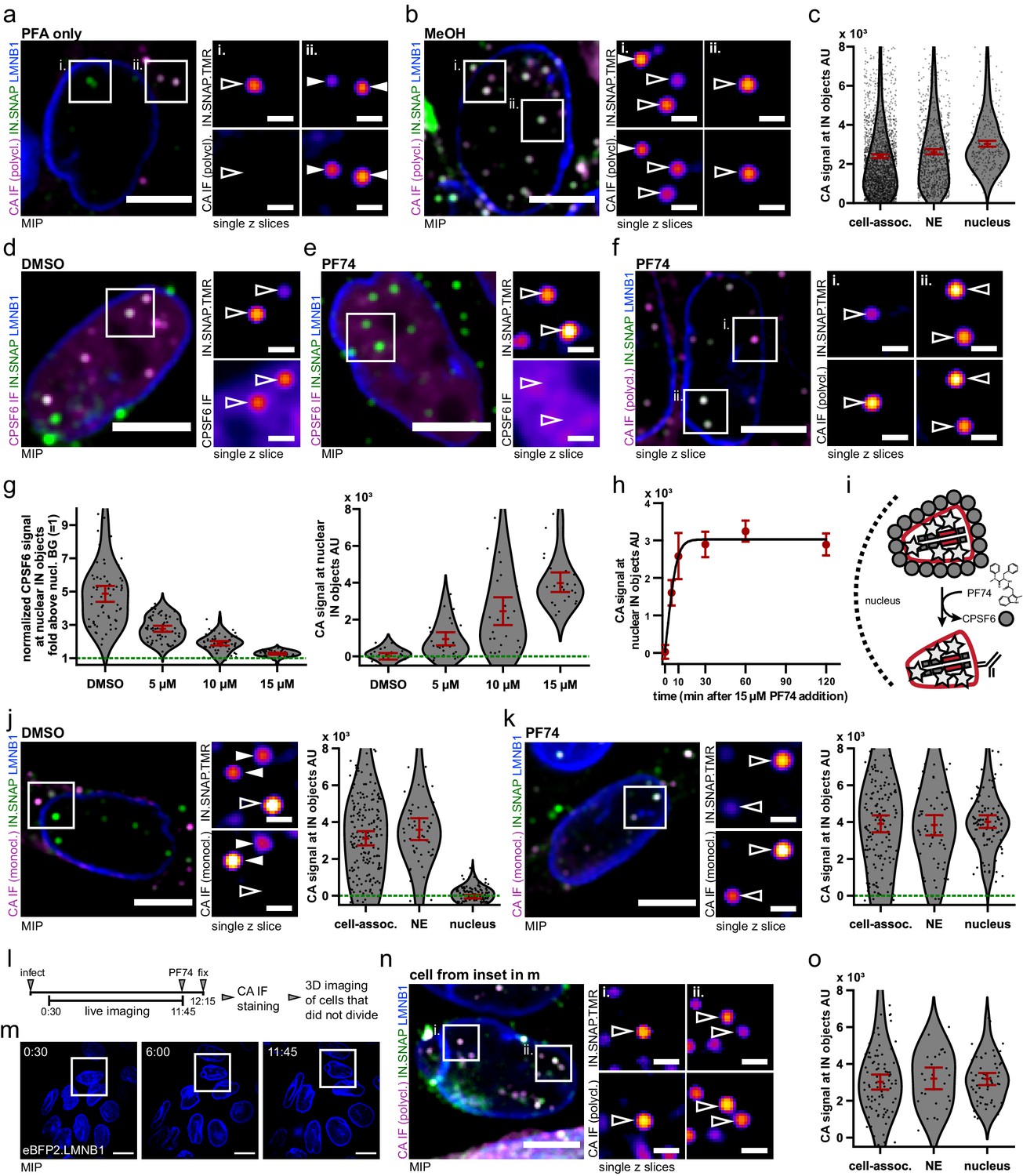



Hiv 1 Uncoating By Release Of Viral Cdna From Capsid Like Structures In The Nucleus Of Infected Cells Elife




Are Gastrointestinal Symptoms Specific For Coronavirus 19 Infection A Prospective Case Control Study From The United States Gastroenterology
5 12 13 üçgeni şükela tümü bugün (bkz pisagor üçlüleri ) (bkz özel üçgenler ) 23, 67 ve 90 derecelik iç açılara sahip özel üçgen dir üçgenlerin kralı hem 12 var içinde hem 13 hem de dik bi üçgenden başka ne istenebilir ki? 16 Özel Üçgenler DİK ÜÇGEN Bir açısının ölçüsü 90° olan üçgene dik üçgen denir Dik üçgende 90° nin karşısındaki kenara hipotenüs, diğer kenarlara dik kenar adı verilir Hipotenüs üçgenin daima en uzun kenarıdırşekilde, m (A) = 90° BC kenarı hipotenüs AB ve AC kenarlarıdik kenarlardırA) 10 B) 11 C)12 D) 13 E) 14 Yukarıda verilenlere göre, x kaç cm dir?



15 75 90 Ucgeni Ozellikleri




Dershane Osym Lys Ygs Video Ders Konu Anlatim Izle On The App Store
özel bir dik üçgendir 90 derecelik açının karşısında hipotenüs bunulunur Bu 90 derecelik açının olduğu yerden hipotenüse indirilecek dik (yani yükseklik) h olursa hipotenüs de 4h olacaktır 5 ayrıca 75 ten uzatılacak kol ile 15 15 eş üçgeni ve 30 60 90 dik üçgeniDik Üçgen, Pisagor Bağıntısı, Özel Dik Üçgenler, İkizkenar dik üçgen, (30° – 60° – 90°) Üçgeni, (30° – 30° – 1°) Üçgeni, (15° – 75° – 90°) Üçgeni, Öklit Bağıntıları, İkizkenar Üçgen, Eşkenar Üçgen vb içerikler hakkında detaylı bilgileri bulabilirsiniz(15 75 90) Üçgeni (15 75 90) Üçgeni konusunu önce anlatıyoruz hemen ardından etkileşime geçmesini sağlıyoruz Bu şekilde kalıcılığı ve öğrenmeyi sağlıyoruz
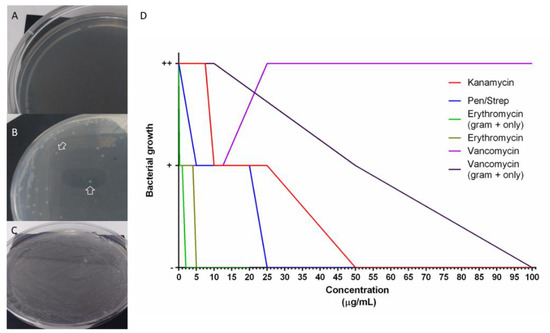



Biology March 21 Browse Articles



1
15 75 90 üçgeni, üçgenler geometrinin temelini oluşturmaktadır Düzlemde doğrusal olmayan 3 noktanın birleşmesi ile oluşan geometrik şekildir Üç kenarı ve üç köşesi bulunan üçgenlerin 4 çeşidi bulunmaktadır Çeşitkenar üçgen, ikizkenar üçgen ve eşkenar üçgendNotKonu Anlatım Videosu Sayfanın sonundadır Pisagor Bağıntısı Bir dik üçgende;12 A B C E 75 15 H 15 x EH = x uzunluğudur Buradan AB = 4 EH olduğundan, 12 = 4 x x = 3 br bulunur Cevap A'dır (vii)(30 30 1 ) ÜÇGENİ A B C 30 30 1




Opportunities And Challenges In The Therapeutic Activation Of Human Energy Expenditure And Thermogenesis To Manage Obesity Journal Of Biological Chemistry



Academic Oup Com Mnras Article Pdf 494 2 12 Staa8 Pdf
Özel üçgenlerden bilinmesi gereken üçgenlerden bir tanesi de 15 75 90 üçgenidir Bu üçgenin bilinmesi soruların çözülmesi açısından basitlık sağlamaktadır 15 75 90 üçgeni bir dik üçgendir Her üçgende olduğu gibi iç açıları toplamı 180, dış açıları toplamı ise 360 derecedir Bu dik üçgende kenar uzunlukları için Pisagor teoremi uygulanmaktadır 15 7515 75 90 Üçgeni Logaritma Kuralları (Logaritma Özellikleri) Sabit Polinom Nedir ?Dik kenarların uzunluklarının kareleri toplamı, hipotenüs uzunluğunun karesine eşittir Yukarıda verilenlere göre, x kaç cm dir?
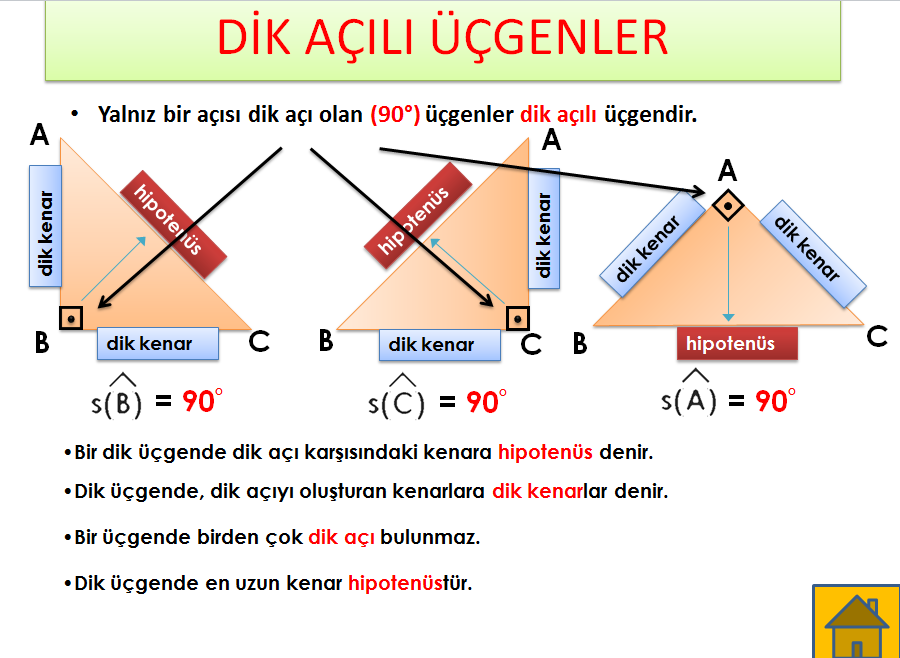



Dik Acili Ucgenin Kenar Ve Aci Ozellikleri Nedir




15 75 90 Ucgeni Kurali Nedir 15 75 90 Ozel Ucgeni Ozellikleri Ve Ornek Sorular Egitim Haberleri
Dik üçgenin alanı öğrenilirken aşağıdaki formül kullanılmaktadır Bu formül; Üçgeni Bu üçgende 15°'lik açının karşısındaki kenar 1 cm ise 75°'lik kenarın karşısındaki kenar cm olur İspatı ise 22,567,590 üçgenindeki gibidir Tek farkı, 75°'lik açının 15° ve 60°'lik açılara bölünmesidir Ayrıca bu üçgende hipotenüse indirilen dikme, hipotenüsün 1/4 katıdır75 8a 75 a olur 30Bulunan a değeri denklemde yerine yazılırsa, x 16 75 8 15 x 16 8 15 x 16 a 15 x 10 x 16 5 8 olur Cevap D'dir 9 İç açıortay teoreminden AN = 5k, NB = 3k diyebiliriz ek ildeki üçgen (3 4 5) üçgeni olduğuna göre, AB = 12 cm dir 5k 3k = 12 3 k A B 9 C 15 N 3k 5k 2 3 15 5 cm olur ANC üçgeninin alanı =




Small Dense Low Density Lipoprotein Cholesterol Is The Most Atherogenic Lipoprotein Parameter In The Prospective Framingham Offspring Study Journal Of The American Heart Association
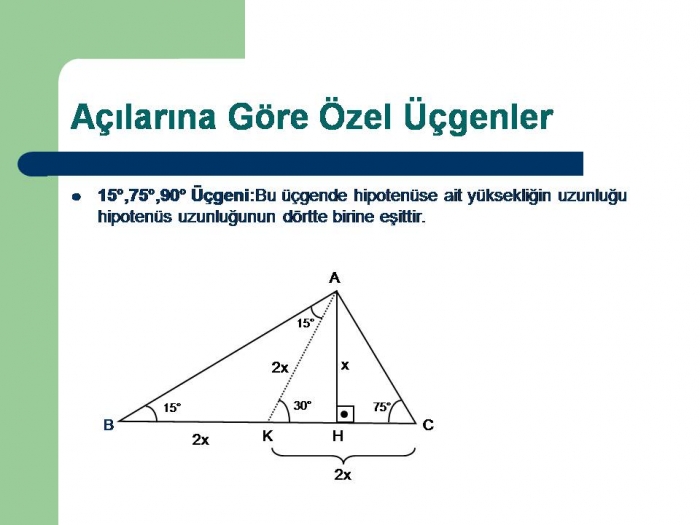



15 75 90 Ucgeni Uludag Sozluk
Düzgün altıgenin alanını 75 cm 2 bulduysanız ve eksik üçgenin alanını ise 15 cm 2 bulduysanız bu durumda yapmanız gereken 75 – 15 işleminin sonucu hesaplamak ve 60 bulmaktır Düzgün olmayan altıgenin alanı 60 cm 2 olarak bulunur Düzgün altıgen özelikleri Tüm kenarları eşit uzunluktadır Tüm iç açıları Son olarak 3 4 5 üçgeninin trigonometrik bağıntılarını da paylaşalım Sin37 = 3 / 5 = 0,6 Sin53 = 4 / 5 = 0,8 Cos37 = 4 / 5 = 0,8 Sin53 = 3 / 5 = 0,6 Tan37 = 3 / 4 = 0, 75 Tan53 = 4 / 3 3 4 5 üçgeni soruları sadece geometride değil aynı zamanda fizikte de karşımıza çıkmaktadır Bu nedenle bu üçgenin açı veKenar uzunlukları tamsayı olan bazı dik üçgenler aşağıda verilmiştir



What Are The Side Relationships Of A 15 75 90 Triangle Quora




Dik Ucgen Konu Anlatimi Ve Ornek Soru Cozumu Kunduz
15 75 90 özel üçgeni özellikleri ve örnek sorular ABONE OL Üçgenler geometride ve hayatın birçok alanında karşımıza çıkmaktadır (30° – 30° – 1°) Üçgeni(30° 30° 1°) üçgeninde 30° lik açıların karşılarındaki kenarlara a dersek 1° lik açının karşısındaki kenar aÖ3 olur 6 (15° – 75° – 90°) Üçgeni (15° – 75° – 90°) üçgenindehipotenüse ait yükseklik AH = h dersek, hipotenüs 15 75 90 Üçgeni Kuralları 15 75 90 üçgeni özellikleri çoğu zaman dik bir üçgene dikme indirildiğinde ortaya çıkar Görselden de gördüğünüz gibi dik üçgenin, dik açısından tabana doğru bir dikme indirilmiş Daha sonra karşımıza iki adet 15 75 90 üçgeni çıkmış




The Urban Crime And Heat Gradient In High And Low Poverty Areas Sciencedirect
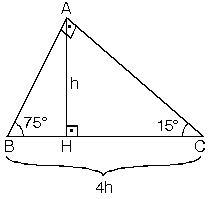



Dik Acili Ucgenin Kenar Ve Aci Ozellikleri Nedir
15 75 90 üçgeni 2 ayrı çözüm yöntemi bulunur bunlardan bir tanesi 75 derecelik açıyı 30 ve 45 olarak, diğeri de 15 ve 60 olarak bölmektir 30 ve 45 olar (15 75 90) Üçgeni (45 45 90) Üçgeni;A) 4 B) 6 C) 8 D) 9 E) 12 ÇÖZÜM 2 AED üçgeninin alanı ile DEC üçgeninin alanı aynıdır (Çünkü tabanları ortak ve yükseklikleri eşittir) ECB üçgeni 15 75 90 üçgeni olduğu için, yükseklik 1 hipotenüsün ü dür 4 cm olur 4 A(DEC) 12 cm is e x4 12 4x 24 x 6 cm buluruz 5 (30° – 30° – 1°) Üçgeni (30° – 30° – 1°) üçgeninde 30° lik açıların karşılarındaki kenarlara a dersek 1° lik açının karşısındaki kenar aÖ3 olur 6 (15° – 75° – 90°) Üçgeni (15° – 75° – 90°) üçgeninde hipotenüse ait yükseklik AH = h




Ontogenetic Timing As A Condition Dependent Life History Trait High Condition Males Develop Quickly Peak Early And Age Fast Hooper 17 Evolution Wiley Online Library



15 75 90 Ucgeni Kenar Bagintisi Ispat
Dairede Alan (İSPAT) Üçgeni Kenar Bağıntısı ( İSPAT ) Heronİç teğet çember arasındaki güzel bir ilişki;7 (30° 30° 1°) Üçgeni (30° 30° 1°) üçgeninde 30° lik açıların karşılarındaki kenarlara a dersek 1° lik açının karşısındaki kenar a 3 olur 8 (15° 75° 90°) Üçgeni (15° 75° 90°) üçgeninde hipotenüse ait yükseklik AH = h dersek, hipotenüs BC = 4h olurBu ders notumuzda Geometri dersinin Özel Üçgenler başlığı altında;
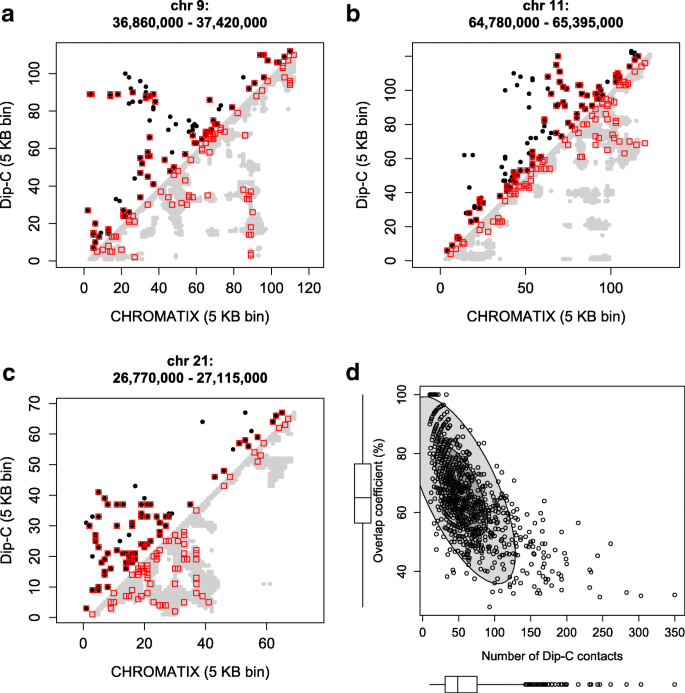



Chromatix Computing The Functional Landscape Of Many Body Chromatin Interactions In Transcriptionally Active Loci From Deconvolved Single Cells Genome Biology Full Text
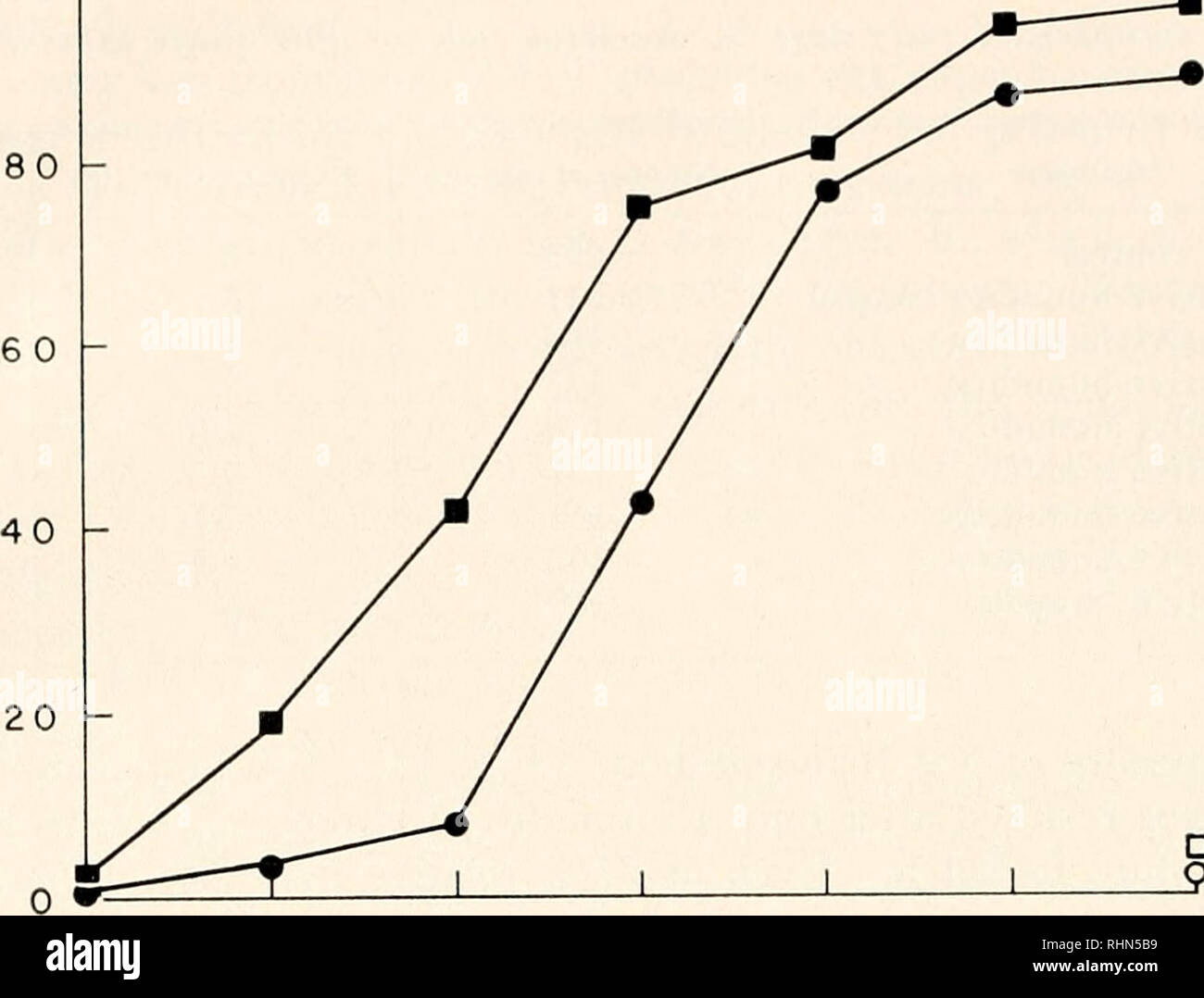



Capsules R High Resolution Stock Photography And Images Page 2 Alamy
Bulunur ABE üçgeni (15 75 90 ) üçgenidir ABE üçgeninde E nin AB ye en yakın uzaklığı hipotenüse ait yükseklik; (30° – 30° – 1°) Üçgeni (30° – 30° – 1°) üçgeninde 30° lik açıların karşılarındaki kenarlara a dersek 1° lik açının karşısındaki kenar a Ö 3 olur 6 (15° – 75° – 90°) Üçgeni (15° – 75° – 90°) üçgenindeüçgen, doğrusal olmayan üç noktayı ikişer ikişer birleştiren doğru parçalarının oluşturduğu şekle denir Geniş açılı üçgen ise, açılarından birinin 90 dereceden büyük yani geniş açı olan üçgene geniş açılı üçgen denirBir üçgen düzleminde b




Dik Ve Ozel Ucgenler



Www Medrxiv Org Content 10 1101 11 30 v3 Full Pdf
(30° – 30° – 1°) Üçgeni(30° – 30° – 1°) üçgeninde 30° lik açıların karşılarındaki kenarlara a dersek 1° lik açının karşısındaki kenar aÖ3 olur 6 (15° – 75° – 90°) Üçgeni (15° – 75° – 90°) üçgeninde hipotenüse ait yükseklik AH = h dersek, hipotenüsBC = 4h olurDik üçgenlerde hipotenüse ait yüksekliğin verildiği durumlarda benzerlikten kaynaklanan öklit Bu yazımızda 30 60 90 Üçgeni, 45 45 90 Üçgeni, 30 30 1 Üçgeni, 15 75 90 Üçgeni, Üçgende İç Açılar Toplamı, Dış Açılar Toplamı, Roket Kuralı ve çok daha fazlası hakkında bilmen gerekenler ile Üçgende Açılar konusuna ait soruları çözerken işine yarayacağını düşündüğümüz ipuçları yer alıyor Umarız
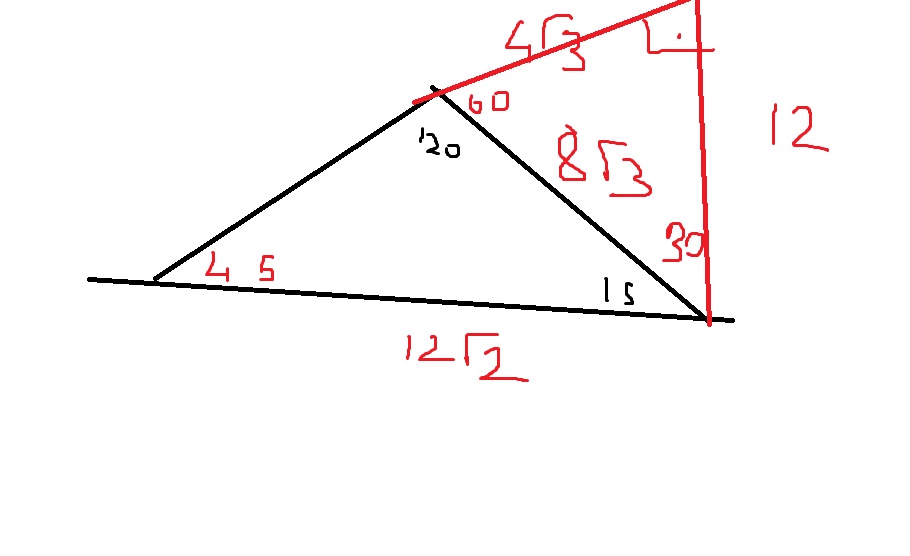



15 75 90 Ucgeni




Ucgenin Alani Nasil Bulunur Ucgen Alan Formulleri Ve Cesitleri Bilgeniz Com
15 75 90 üçgeni kuralı nedir ?Yükseklik aynı olduğu için alanlar arasında taban uzunlukları ile orantılı bir durum vardır Bu soru 1998 yılında üniversite sınavında çıkmıştır ABD üçgenin alanı 6 cm 2 olduğu verilmiş ve ABC üçgeninin alanı sorulmuştur Oran mantığı ile ADC üçgeni 24 cm 2 olacak ve büyük üçgen de 30 cm 2 olacaktır Soru5 birimlik kenarın karşısı 23, 12 birimlik kenarın karşısı 67, 13 birimlik




Revisiting Hydrometeorology Using Cloud And Climate Observations In Journal Of Hydrometeorology Volume 18 Issue 4 17




Geometri Sorularim 9 Adet




Effectiveness Of Non Pharmaceutical Interventions To Contain Covid 19 A Case Study Of The Spring Pandemic Wave In New York City Journal Of The Royal Society Interface




Laparoscopic Guided Transversus Abdominis Plane Block For Postoperative Pain Management In Minimally Invasive Surgery Systematic Review And Meta Analysis Journal Of The American College Of Surgeons



Page 9 15 7 98 High Resolution Stock Photography And Images Alamy




15 75 90 Ozel Ucgeninin Kenar Bagintilari Nedir Eodev Com




Comparison Of Cumulative Clinical Benefits Of Biologics For The Treatment Of Psoriasis Over 16 Weeks Results From A Network Meta Analysis Journal Of The American Academy Of Dermatology




Dik Ucgen 17 22 5 67 5 90 Ucgeni Evde Egitim Matematik Ders Calisma Ipuclari



Soft And Flexible Piezoelectric Smart Patch For Vascular Graft Monitoring Based On Aluminum Nitride Thin Film Scientific Reports
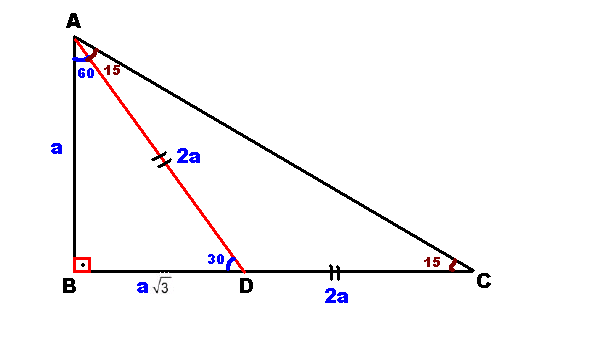



15 75 90 Ucgeni 2 3 Ispat




Comparison Of Global Precipitation Estimates Across A Range Of Temporal And Spatial Scales In Journal Of Climate Volume 29 Issue 21 16




15 75 90 Ucgeni Webders Net



Developmental Criminology And The Crime Decline




15 75 90 Ucgeni Ozellikleri Ve Kurali Ogrenci Yardim




Ozel Ucgenler Nelerdir Ozel Ucgenler 8 15 17 7 24 25 30 60 90 Ve Diger
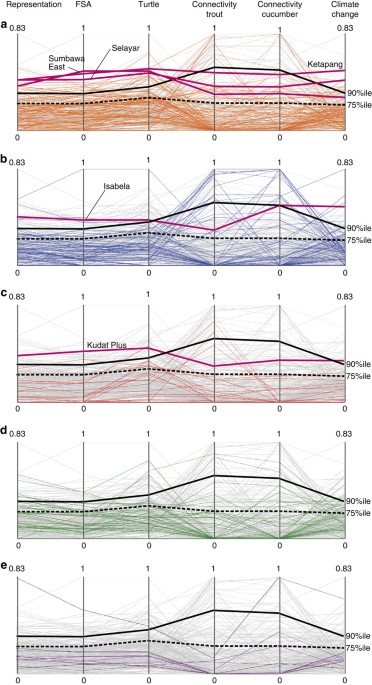



Integrating Regional Conservation Priorities For Multiple Objectives Into National Policy Nature Communications




A Signature Based Machine Learning Model For Distinguishing Bipolar Disorder And Borderline Personality Disorder Translational Psychiatry
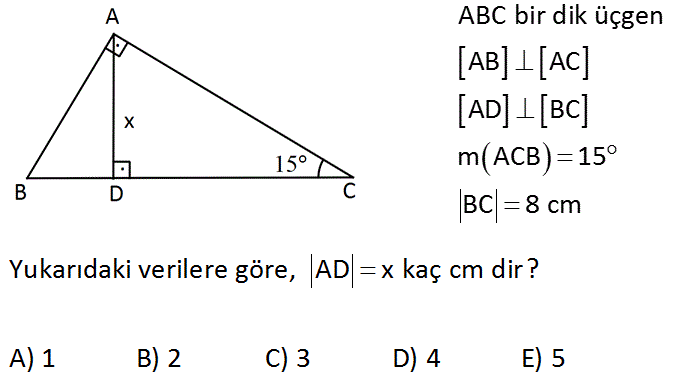



15 75 90 Ucgeni
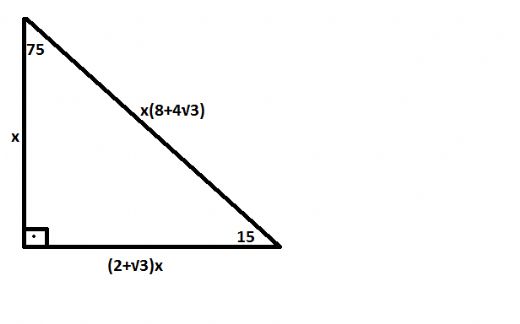



15 75 90 Ucgeninin Ozellikleri Nelerdir




Non Steroidal Anti Inflammatory Drug Use And Outcomes Of Covid 19 In The Isaric Clinical Characterisation Protocol Uk Cohort A Matched Prospective Cohort Study The Lancet Rheumatology




15 75 90 Ucgeni Akilli Geometri




Dik Ucgenler Pisagor Teoremi Konu Anlatimi Soru Cozumleri Ders Notu 9 Sinif Matematik Tyt




Acilar Ve Ucgenler




15 75 90 Ucgen Ozelligi Ve 5 Ornek Cozum Youtube




Potential Ecological Impacts Of Climate Intervention By Reflecting Sunlight To Cool Earth Pnas




Dik Ucgen 15 75 90 Ucgeni Islemli Em Iyi Secicem Gereksiz Engellenir Eodev Com
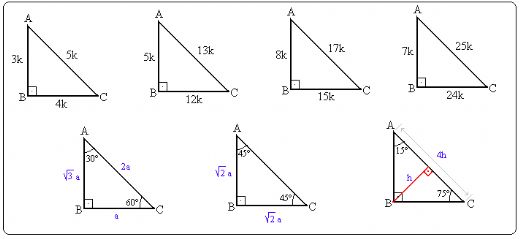



Ucgende Yukseklik Hesaplamasi
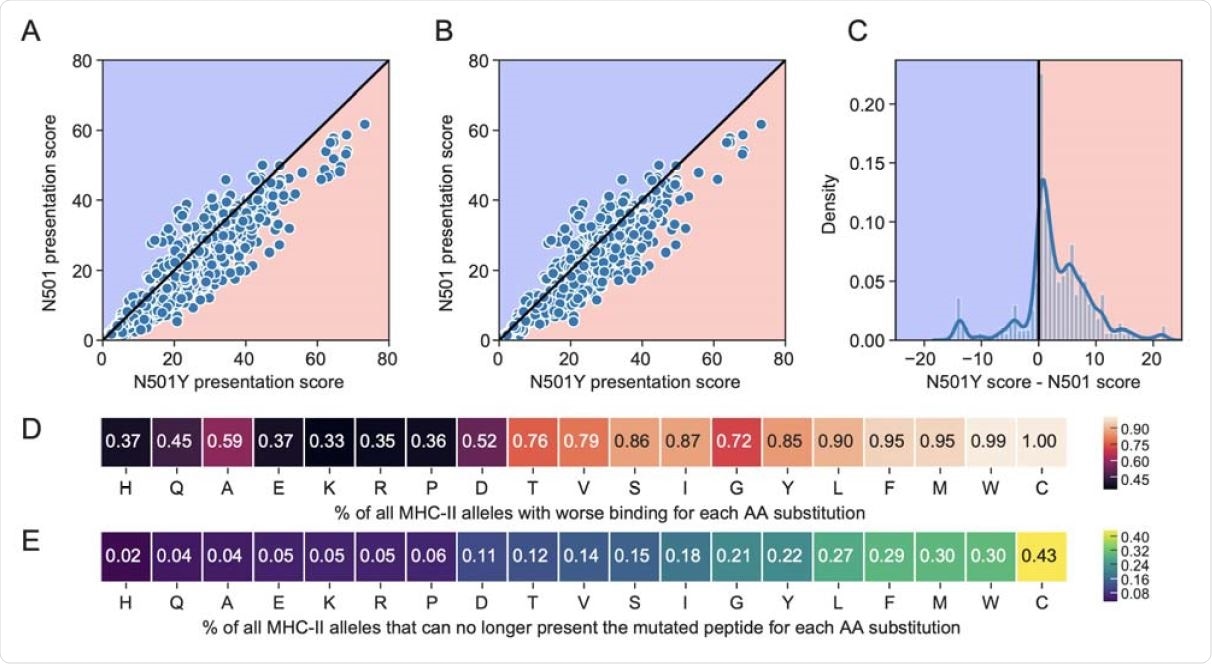



Sars Cov 2 N501y Mutation Adversely Affects Cellular Immune Response
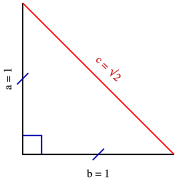



Dik Ucgen Vikipedi




Economists And Public Opinion Expert Consensus And Economic Policy Judgments The Journal Of Politics Vol 78 No 2




Britain S One Jab Strategy The New York Times




Dik Ucgen 5 45 45 90 Ucgeni Geometri Metin Hocam Youtube
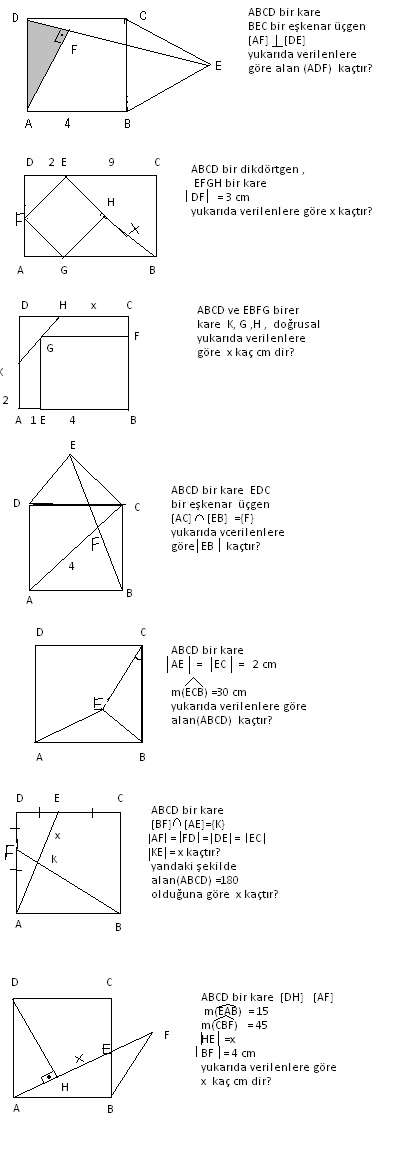



Kare Sorulari Lutfen Yardimci Olurmusunuz Acillll




30 60 90 Ucgeni Ve Ozellikleri Not Bu




Sozel Geometri Sorulari Pdf Ucretsiz Indirin



1




15 75 90 Ucgeni Not Bu




Non Canonical Metabolic Pathways In The Malaria Parasite Detected By Isotope Tracing Metabolomics Molecular Systems Biology



Dik Acili Ucgenin Kenar Ve Aci Ozellikleri Nedir




Page 3 Bookleafnumber111 High Resolution Stock Photography And Images Alamy




Acb Ucgen Alani Buldum Adc Ucgeni 15 75 90 Icin De Sadece Yerlestirmeyi Yapamadim Bakar Misinz Eodev Com




Origins Of Felsic Magmas In Japanese Subduction Zone Geochemical Characterizations Of Tephra From Caldera Forming Eruptions 5 Ma Kimura 15 Geochemistry Geophysics Geosystems Wiley Online Library
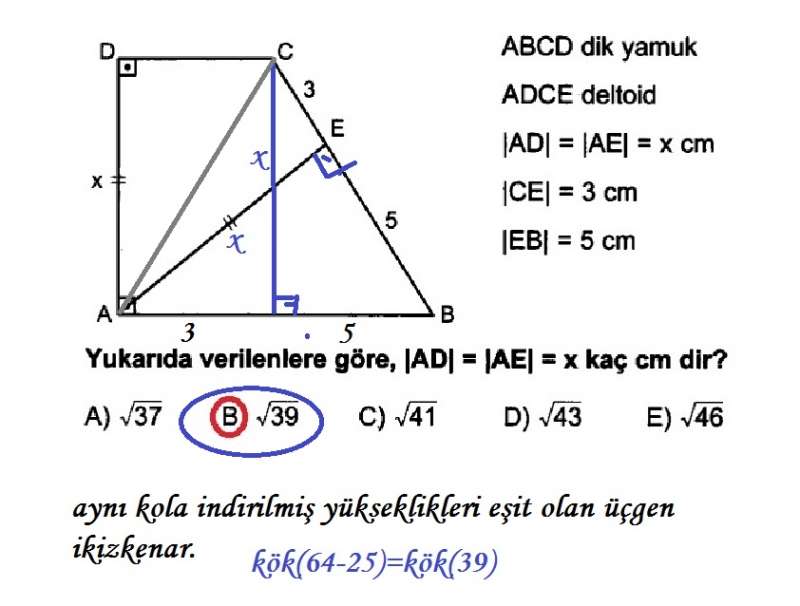



Yamuk




15 75 90 Ucgeninin Ozelligi Nedir Eodev Com




15 75 90 Ucgeni Eodev Com



1




Dik Ucgen 16 15 75 90 Ucgeni Temel Matematik Matematik Felsefesi Evde Egitim




15 75 90 Ucgeni Ucgende Acilar Ders Notlari Kunduz



15 75 90 Ucgnler Sitem
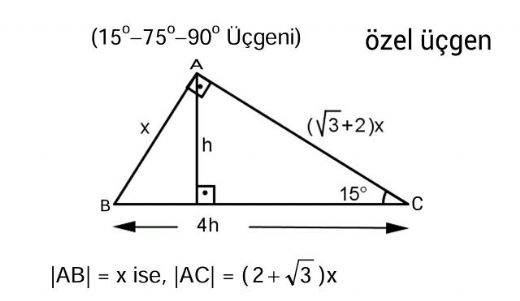



90 75 15 Ucgeni Ozellikleri
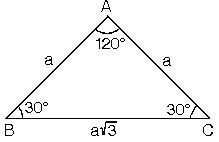



Dik Acili Ucgenin Kenar Ve Aci Ozellikleri Nedir




15 75 90 Ucgeni Ozellikleri Ve Kurali Soru List
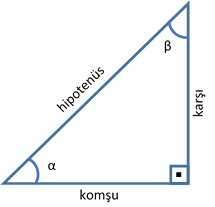



Dik Ucgende Trigonometrik Hesaplamalar




15 75 90 Ucgeni Pow Bylge




Dik Ucgen Vikipedi
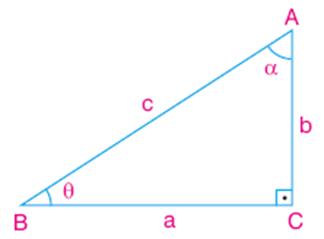



Dik Ucgende Trigonometrik Oranlar




Dik Ucgen Konu Anlatimi Ve Ornek Soru Cozumu Kunduz




Sinavlarda Hic Sorulmadi Sorarlar 22 5 67 5 90 Ucgeni Youtube




Directional Semivariogram Analysis To Identify And Rank Controls On The Spatial Variability Of Fracture Networks Sciencedirect




Process Intensification Of Continuous Antisolvent Crystallization Using A Coiled Flow Inverter Industrial Engineering Chemistry Research




30 30 1 Ucgeni Kenar Iliskisi Ve Alan Formulu Ispati Youtube




Ozel Ucgenler
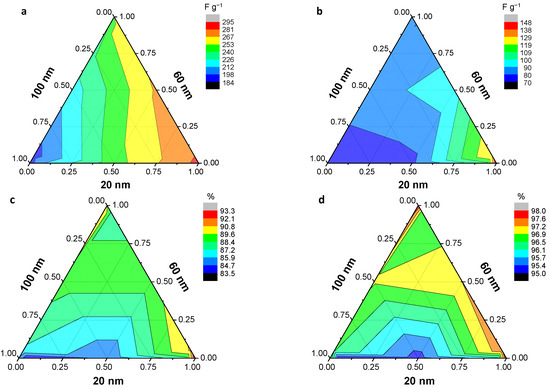



Polymers Free Full Text Electrical And Electrochemical Properties Of Conducting Polymers Html




Development And Validation Of The Isaric 4c Deterioration Model For Adults Hospitalised With Covid 19 A Prospective Cohort Study The Lancet Respiratory Medicine
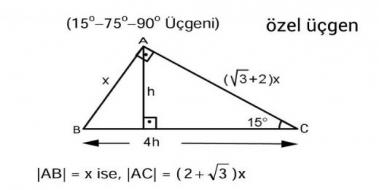



Populer Icerik




Group Loyalty And The Taste For Redistribution Journal Of Political Economy Vol 109 No 3



1




Dik Ucgen 16 15 75 90 Ucgeni Temel Matematik Matematik Felsefesi Evde Egitim




Comparative Effectiveness Of Sleep Apnea Screening Instruments During Inpatient Rehabilitation Following Moderate To Severe Tbi Archives Of Physical Medicine And Rehabilitation



Dik Ucgen Vikipedi




The Osmolyte Tmao Modulates Protein Folding Cooperativity By Altering Global Protein Stability Biochemistry
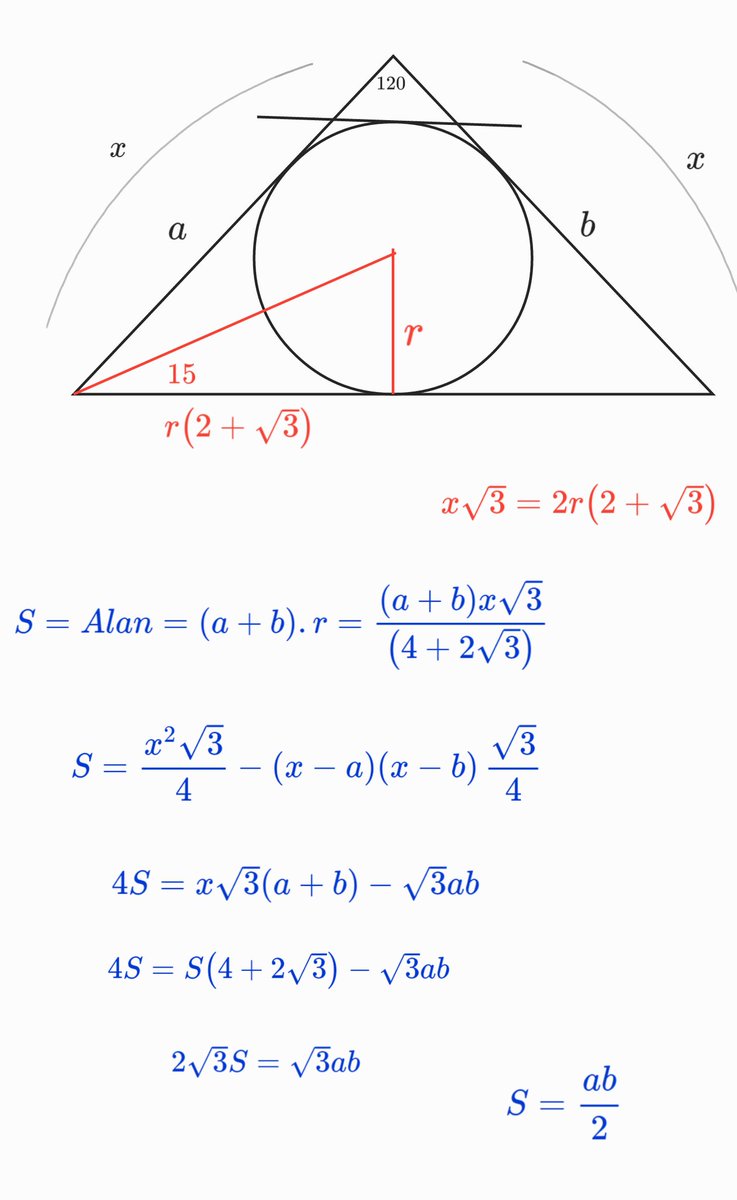



Fatih Saglam Gece Gece Iyi Geldi Kafadagitmaca Bunlarda Ispatlar Cos Teoremi Alanlar Farki Tegetler Dortgeni 15 75 90 Tesekkurler Galois1724 T Co 6fpvza795u T Co Sd9h6pyqqb




15 75 90 Ucgeni Ozelliklerinin Ispati Youtube
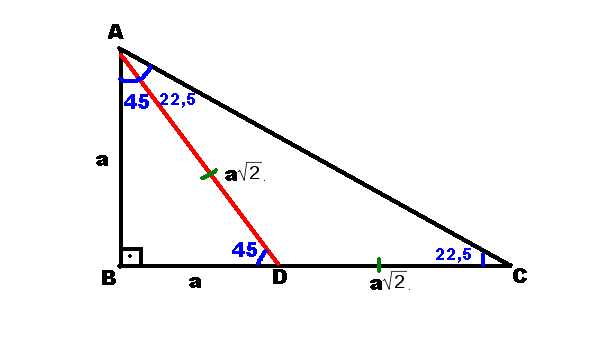



22 5 67 5 90 Ucgeni 1 2 Ispat




Dik Ucgen Konu Anlatimi Ve Ornek Soru Cozumu Kunduz




Ucgenler Icin 76 Fikir Evde Egitim Matematik Geometri



0 件のコメント:
コメントを投稿